LIMIT DAN FUNGSI
Limit fungsi adalah konsep fundamental dalam kalkulus dan analisis mengenai aturan bahwa suatu fungsi mendekati suatu input tertentu. Limit biasa digunakan untuk menyatakan batas. Artinya kita boleh mendekati batas tersebut tetapi tidak boleh mencapai batas tersebut.
1. Definisi Limit Fungsi Secara Informal
Definisi limit fungsi secara informal adalah ketika sebuah fungsi f memberikan sebuah output f(x) untuk setiap input x, fungsi tersebut memiliki limit L pada sebuah input p. Ini berarti f(x) mendekati L ketika x mendekati p. Lebih spesifik lagi, ketika f diterapkan untuk setiap input yang mendekati p, maka nilai output mendekati L.
2. Definisi Limit Fungsi Secara Formal

Persamaan diatas adalah definisi limit fungsi secara formal. Dimana f(x) dapat dibuat sedekat dengan L dengan membuat x mendekati p, tetapi tidak sama dengan p.
3. Definisi Limit Menurut Austin Louis Cauchy
Berikut adalah definisi limit menurut Austin Louis Cauchy:
Sebuah fungsi f(x) mempunyai  jika dan hanya jika untuk sembarang bilangan real
jika dan hanya jika untuk sembarang bilangan real  maka terdapat bilangan real
maka terdapat bilangan real  sedemikian hingga memenuhi:
sedemikian hingga memenuhi:
" cara membaca Limit dan fungsi "
Dalam matematika, limit dapat dikatakan sebagai prediksi nilai ordinat yang didapat pada suatu titik. Nilai limit diperoleh dengan pendekatan dari sisi kanan dan sisi kiri. Jika nilai limit dari kiri sama dengan nilai limit dari kanan maka fungsi f(x) mempunyai nilai limit. Notasi limit dismibolkan pada persamaan di bawah.

Cara membaca notasi limit di atas adalah nilai limit f(x) untuk x mendekati a dinyatakan dalam sebuah nilai yang terletak pada ordinat (y). Secara baku, limit dinyatakan melalui definisi di bawah.
Penjelasan mengenai limit untuk lebih detailnya akan diberikan melalui beberapa kasus yang akan diberikan di bawah.
Nilai Limit Terdefinisi di Semua Titik
Bagaimana cara mencari nilai limit?
Nilai limit diperoleh melalui pendekatan dari kiri dan kanan. Secara sederhana, limit dapat diartikan sebagai nilai y yang merupakan prediksi dari nilai suatu fungsi di suatu titik.
Ulasan pertama yang akan dibahas adalah menentukan nilai limit pada grafik linear. Seperti kita tahu bahwa grafik linear terdefinisi di semua titik. Perhatikan grafik fungsi linear di bawah.
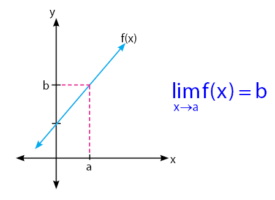
Berdasarkan grafik di atas, nilai x terdefinisi di semua titik. Nilai limit f(x) untuk x mendekati a dari kanan adalah b dan nilai limit f(x) untuk x mendektai a dari kiri adalah b. Sehingga, kesimpulan yang dapat diambil adalah nilai limit f(x) adalah b.
Contoh kasus pertama ini merupakan kasus sederhana tentang limit karena diberikan grafik linear yang nilai x terdefinisi di semua titik
Pada pembahasan limit, kita tidak melihat apa yang terjadi pada satu titik, tapi melihat nilai yang dapat terjadi di sekitar titik ketika didekati sangat dekat dari kiri dan dari kanan. Kondisi tertentu dapat memungkinkan grafik yang nilai x tidak terdefinisi di suatu titik. Namun, tidak mustahil jika nilai limitnya sama dengan grafik yang terdefinisi di semua titik.
Untuk lebih jelasnya, perhatikan grafik yang diberikan pada gambar di bawah.

Grafik di atas tidak terdefinisi pada titik x = a. Namun, ketika fungsi f(x) didekati dari kiri, nilainya akan menuju titik b. Begitu juga ketika f(x) didekati dari kanan, nilainya akan menuju titik b. Kesimpulannya, nilai limit f(x) adalah b.

Sebagian orang mungkin menanyakan, mengapa jika nilai limit merupakan nilai yang diperoleh dari pendekataan, notasi limit disimbolkan dengan tanda sama dengan?
Hal ini dikarenakan penyimbolan limit memang dibuat seperti demikian. Ini merupakan simbol notasi limit, tidak ada alasan lain.
Nilai Llimit Tidak Ada
Ada sebuah kondisi tertentu, di mana nilai limit f(x) yang didekati dari kiri tidak sama dengan nilai limit yang didekati dari kanan. Kondisi ini tentunya tidak akan menghasilkan nilai limit. Untuk lebih jelasnya, perhatikan grafik di bawah.

Untuk mendapatkan nilai limit f(x) di titik x = a, sobat idschool perlu mencari tahu nilai limit f(x) jika x didekati dari kiri dan kanan. Selanjutnya, sobat idschool perlu membandingkan nilai limit f(x) untuk x mendekati a dari kiri dan untuk x mendekati a dari kanan.
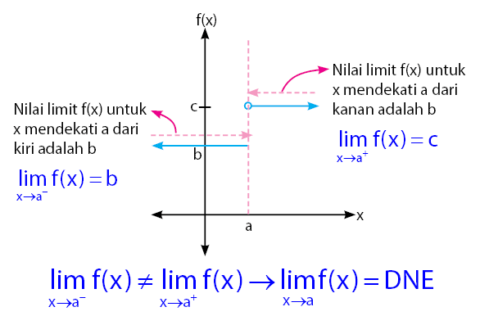
Berdasarkan grafik yang diberikan di atas, untuk x mendekati a dari kiri, nilai limitnya adalah b, sedangkan untuk x mendekati a dari kanan, nilai limitnya adalah c.
Kita mendapatkan nilai limit f(x) untuk x mendekati a dari kiri tidak sama dengan nilai limit f(x) untuk x mendekati a dari kanan. Kesimpulanya, nilai limit f(x) tidak ada, biasa ditulis dengan DNE (Do Not Exist).
Selanjutnya, ulasan kasus yang ke tiga adalah nilai limit untuk x mendekati tak hingga  dan x mendekati negatif tak hingga
dan x mendekati negatif tak hingga  .
.
Nilai Limit di Tak Hingga
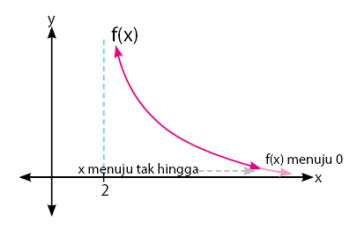
Ulasan yang akan dibahas di sini adalah cara menentukan nilai limit fungsi jika x mendekati tak hingga. Untuk mengetahui caranya, perhatikan gambar grafik fungsi f(x) dan g(x) yang diberikan di bawah.

Nilai limit f(x) untuk x mendekati tak hingga, nilainya adalah 0. Hasil ini diperoleh dengan mendekati nillai f(x) ketika x mendekati tak hingga, grafik akan menuju titik 0. Perhatikan grafik di bawah.
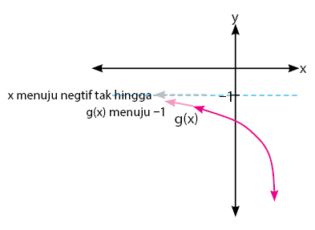
Hampir sama seperti cara di atas, nilai limit g(x) untuk x mendekati negatif tak hingga, nilainya adalah  . Hasil ini diperoleh dengan mendekati nillai f(x) ketika x mendekati negatif tak hingga, grafik akan menuju titik
. Hasil ini diperoleh dengan mendekati nillai f(x) ketika x mendekati negatif tak hingga, grafik akan menuju titik  . Perhatikan grafik di bawah.
. Perhatikan grafik di bawah.
- teknik-teknik subsitusi
- Substitusi nilai limit x pada persamaanCara pertama yang perlu dilakukan untuk mengetahui suatu nilai limit fungsi adalah dengan melakukan substitusi nilai limit x pada persamaan. Jika hasil yang diperoleh adalah suatu nilai, (bukan
) maka proses mencari nilai limit berhenti sampai di sini. Untuk lebih jelasnya, perhatikan contoh cara mencari nilai limit di bawah.
Untuk mendapatkan nilai limit fungsi seperti bentuk di atas, sobat idschool hanya perlu melakukan substitusi nilai x = 4 pada persamaan fungsinya.Proses mencari nilai limit sudah berakhir di sini.Bentuk limit fungsi yang dapat diselesaikan menggunakan substitusi nilai limit x adalah persamaan polinomial, fungsi konstanta, dan bentuk akar nilai positif, dan bentuk pangkat.Bentuk limit fungsi yang dapat diselesaikan menggunakan cara substitusi: - PemfaktoranTips kedua yang dapat digunakan untuk menemukan nilai limit adalah metode pemfaktoran. Cara ini digunakan jika proses pencarian nilai limit dengan metode substitusi menghasilkan nilai
. Seperti terlihat pada contoh di bawah.
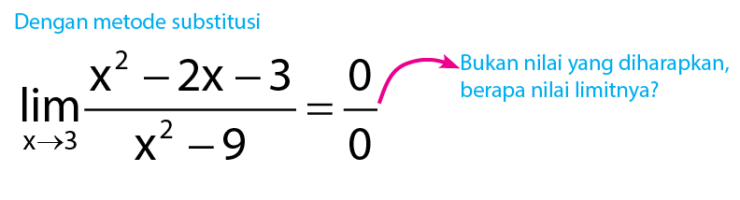 Hasil limit seperti di atas bukan merupakan nilai limit yang diharapkan. Proses mencari nilai limit belum selesai, untuk mencari nilai limit dengan bentuk ini, sobat idschool dapat menggunakan metode pemfaktoran. Perhatikan cara mencari nilai limit dengan metode pemfaktoran yang akan diberikan di bawah.
Hasil limit seperti di atas bukan merupakan nilai limit yang diharapkan. Proses mencari nilai limit belum selesai, untuk mencari nilai limit dengan bentuk ini, sobat idschool dapat menggunakan metode pemfaktoran. Perhatikan cara mencari nilai limit dengan metode pemfaktoran yang akan diberikan di bawah. Nilai limit di atas merupakan nilai yang diharapkan. Sekarang, perhatikan bentuk limit fungsi yang diberikan di bawah.
Nilai limit di atas merupakan nilai yang diharapkan. Sekarang, perhatikan bentuk limit fungsi yang diberikan di bawah. Tidak semua bentuk limit fungsi yang diselesaikan menggunakan pemfaktoran akan menghasilkan nilai limitnya. Pada kasus tertentu, ada bentuk limit fungsi yang tidak memiliki nilai limit fungsi. Beberapa contoh nilai limit fungsi yang tidak memiliki nilai dapat disimak berikut.
Tidak semua bentuk limit fungsi yang diselesaikan menggunakan pemfaktoran akan menghasilkan nilai limitnya. Pada kasus tertentu, ada bentuk limit fungsi yang tidak memiliki nilai limit fungsi. Beberapa contoh nilai limit fungsi yang tidak memiliki nilai dapat disimak berikut. Sekarang, idschool akan mengulas bentuk limit yang dapat dikerjakan dengan mengalikan.
Sekarang, idschool akan mengulas bentuk limit yang dapat dikerjakan dengan mengalikan. - Mengalikan dengan Penyebut yang SamaMetode untuk menentukan nilai limit yang ke tiga adalah mengalikan dengan penyebut. Perhatikan bentuk limit yang diberikan pada persamaan di bawah!
 Penyelesaian bentuk limit di atas menggunakan metode substitusi menghasilkan nilai
Penyelesaian bentuk limit di atas menggunakan metode substitusi menghasilkan nilai. Sedangkan metode pemfaktoran juga tidak dapat digunakan karena tidak ada bentuk yang bisa difaktorkan. Sehingga, untuk mendapatkan nilai limit fungsi bentuk ini diperlukan metode lain, yaitu metode mengalikan dengan penyebut yang sama.
Bentuk limit di atas dapat diselesaikan dengan cara mengalikan dengan pembilangnya. Proses menentukan nilai limit dengan metode mengalikan dengan penyebut dapat dilihat pada cara di bawah. - Menyederhanakan Bentuk AljabarMetode atau tips ke empat dalam mencari nilai limit adalah membuka tanda kurung kemudian menyederhanakan bentuknya dan menemukan nilai limitnya. Cara ini dapat digunakan untuk mencari nilai limit dengan bentuk seperti di bawah.
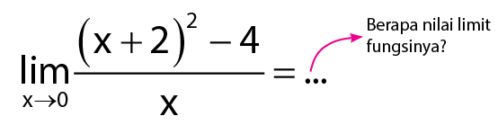 Selalu, dalam proses menemukan nilai limit, sobat idschool perlu cek nilai limit dengan cara substitusi, pemfaktoran, dan mengalikan dengan penyebut yang sama.Hasil substitusi x pada bentuk nilai limit ini tidak menghasilkan nilai limit yang diharapkan, karena menghasilkan nilai
Selalu, dalam proses menemukan nilai limit, sobat idschool perlu cek nilai limit dengan cara substitusi, pemfaktoran, dan mengalikan dengan penyebut yang sama.Hasil substitusi x pada bentuk nilai limit ini tidak menghasilkan nilai limit yang diharapkan, karena menghasilkan nilai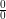 . Seperti terlihat pada cara di bawah.Bentuk limit yang diberikan di atas tidak dapat difaktorkan secara lebih sederhana. Sedangkan metode mengalikan dengan penyebut yang sama juga tidak dapat dilakukan karena tidak ada penyebut sama yang perlu dilakukan. Sehingga, cara menentukan bentuk limit ini adalah dengan membuka tanda kurung dan menyederhanakan bentuk aljabarnya, kemudian menemukan nilai limitnya. Cara menentukan nilai limit bentuk ini dapat dilihat pada cara di bawah.Hasil nilai limit di atas seuai yang diharapkan.
. Seperti terlihat pada cara di bawah.Bentuk limit yang diberikan di atas tidak dapat difaktorkan secara lebih sederhana. Sedangkan metode mengalikan dengan penyebut yang sama juga tidak dapat dilakukan karena tidak ada penyebut sama yang perlu dilakukan. Sehingga, cara menentukan bentuk limit ini adalah dengan membuka tanda kurung dan menyederhanakan bentuk aljabarnya, kemudian menemukan nilai limitnya. Cara menentukan nilai limit bentuk ini dapat dilihat pada cara di bawah.Hasil nilai limit di atas seuai yang diharapkan.
Selain keempat bentuk limit yang telah dibahas di atas, terdapat 3 (tiga) bentuk limit lain. Ketiga bentuk limit tersebut adalah bentuk akar pada pembilang, limit bentuk , dan bentuk limit nilai mutlak.
, dan bentuk limit nilai mutlak. - Menyederhanakan Bentuk Aljabar
- Mengalikan Akar sekawan (conjugate)
Tips menentukan nilai limit ke lima yang akan diulas adalah bentuk limit fungsi yang memiliki akar pada pembilangnya. Contoh bentuk soal yang diselesaikan dengan cara metode ini adalah seperti berikut.

Seperti biasa, kita akan menyelidiki cara menentukan limit dengan cara substitusi, pemfaktoran, dan pembilang yang sama terlebih dahulu.
Pertama, akan diselidiki cara menentukan nilai limit menggunakan metode substitusi.
Hasil yang diperoleh dengan cara di atas tidak sesuai harapan, sehingga perlu dicari menggunakan metode lain.
- perhatikan cara menentukan limit yang akan diberikan pada ulasan di bawah.Kita mendapatkan hasil nilai limit fungsi sesuai harapan.
- Bentuk limit
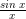 Bentuk limit lainnya adalah bentuk limit fungsi yang mengandung persamaan
Bentuk limit lainnya adalah bentuk limit fungsi yang mengandung persamaan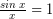 . Sebelum mempelajari lebih jauh tentang bentuk limit fungsi yang memiliki bentuk
. Sebelum mempelajari lebih jauh tentang bentuk limit fungsi yang memiliki bentuk 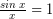 , sobat idschool perlu mengetahui sebuah persamaan limit fungsi berikut.
, sobat idschool perlu mengetahui sebuah persamaan limit fungsi berikut.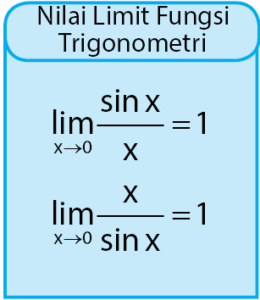 Persamaan di atas dapat digunakan untuk menyelesaikan bentuk limit yang mengandung bentuk
Persamaan di atas dapat digunakan untuk menyelesaikan bentuk limit yang mengandung bentuk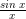 seperti contoh soa yang diberikan di bawah.Cara menyelesakan bentuk soal di atas adalah seperti berikut. Sebelumnya, sobat idschool perlu mengecek contoh menyelidiki nilai limitnya menggunakan metode susbtitusi, pemfaktoran, dan mengalikan dengan penyebut yang sama. Namun, pada pembahasan kali ini akan diskip, mengingat postingan tulisan yang sudah cukup panjang.Sekarang kita akan langsung menentukan nilai limit fungsi yang diberikan di atas.Nilai limit yang diharapkan. Contoh lain akan diberikan seperti di bawah.Contoh lain:Selanjutnya, akan diulas cara menyelesaikan bentuk limit fungsi ke tujuh, yaitu bentuk limit dengan nilai mutlak.
seperti contoh soa yang diberikan di bawah.Cara menyelesakan bentuk soal di atas adalah seperti berikut. Sebelumnya, sobat idschool perlu mengecek contoh menyelidiki nilai limitnya menggunakan metode susbtitusi, pemfaktoran, dan mengalikan dengan penyebut yang sama. Namun, pada pembahasan kali ini akan diskip, mengingat postingan tulisan yang sudah cukup panjang.Sekarang kita akan langsung menentukan nilai limit fungsi yang diberikan di atas.Nilai limit yang diharapkan. Contoh lain akan diberikan seperti di bawah.Contoh lain:Selanjutnya, akan diulas cara menyelesaikan bentuk limit fungsi ke tujuh, yaitu bentuk limit dengan nilai mutlak. - Bentuk Limit Nilai MutlakTips terakhir yang akan diulas pada halaman ini adalah cara menentukan nilai imit fungsi bentuk nilai mutlak. Sebelumnya pahami dulu cara menentukan nilai mutlak yang akan diberikan di bawah.
 Berdasarkan persamaan di atas, kesimpulannya adalah nilai mutlak x akan bernilai x jika
Berdasarkan persamaan di atas, kesimpulannya adalah nilai mutlak x akan bernilai x jika dan nilai mutlak x akan bernilai -x jika
dan nilai mutlak x akan bernilai -x jika  . Selanjutnya, kita akan masuk dalam uasan materi mencari nilai limit fungsi nilai mutak. Perhatikan persamaan di bawah.Berdasarkan cara mencari nilai mutlak, akan diperoleh persamaan sebagai berikut.
. Selanjutnya, kita akan masuk dalam uasan materi mencari nilai limit fungsi nilai mutak. Perhatikan persamaan di bawah.Berdasarkan cara mencari nilai mutlak, akan diperoleh persamaan sebagai berikut.
Nilai limit dari kanan:
Nilai limit dari kiri:Nilai limit dari kanan tidak sama dengan nilai limit dari kiri, sehingga kesimpulannya adalah nilai limit tidak ada. Nilai limit hanya diperoleh ketika nilai limit dari kanan sama dengan nilai limit dari kiri.Jika disajikan dalam gambar akan terlihat seperti berikut.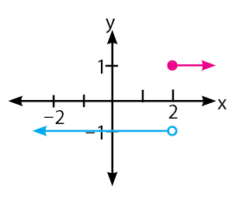
- contoh soal dan penyelesaian nya
1. soal limit dan fungsi :
| Tentukan nilai dari |  |
Pembahasan
Dengan turunan

Tidak ada komentar:
Posting Komentar